La complessa questione della formazione binaria a tre corpi
Il problema dei tre corpi, nato con la teoria della gravitazione newtoniana, rimane ad oggi una delle questioni aperte più complesse in dinamica stellare, la branca dell’astrofisica che studia gli effetti generati dal moto delle stelle e la loro influenza sull’ambiente circostante. La difficoltà nell’individuare una trattazione matematica ad hoc che sia al contempo efficace e poco dispendiosa dal punto di vista computazionale ha sempre introdotto forti limitazioni nell’analisi di certi fenomeni, come la formazione binaria a tre corpi. Ma, se in passato ciò ha costituito un ostacolo quasi insormontabile, ora un ritrovato spirito combattivo sembra diffondersi nel mondo della ricerca grazie alla pubblicazione di un nuovo codice simulativo basato su un metodo d’integrazione diretta all’avanguardia.
La maggioranza delle stelle nell’Universo è parte di sistemi binari: alcune di esse nascono già legate tra loro nella nube molecolare originaria (i.e., binarie primordiali), mentre altre si uniscono nel corso della loro vita per interazione di tipo gravitazionale, soprattutto in ambienti densi come gli ammassi globulari (i.e., binarie dinamiche). A questo proposito, svariati sono i meccanismi che intervengono a vincolare due stelle inizialmente isolate: la frizione dinamica all’interno di un mezzo gassoso, la dissipazione di energia orbitale per effetto delle forze di marea con conseguente restringimento dell’orbita stessa (i.e., cattura mareale), e l’emissione di onde gravitazionali durante il passaggio ravvicinato di due oggetti compatti (i.e, cattura gravitazionale). Inoltre, si riscontra la generazione di sistemi binari anche a seguito dell’incontro fra tre corpi interagenti che subiscono una deflessione delle rispettive orbite e sono perciò indotti ad entrare in contatto tra loro: di essi, uno agisce da catalizzatore trasferendo la propria energia potenziale gravitazionale agli altri due, che la convertono in energia cinetica per associarsi, e venendo espulso al termine del processo. Tale fenomeno, chiamato formazione binaria a tre corpi (i.e., three-body binary formation, 3BBF), è però generalmente poco indagato rispetto a quelli summenzionati. La mancanza d’interesse per la 3BBF si deve alla storica credenza che il suo tasso di produzione di sistemi binari sia globalmente trascurabile, ovvero non rilevante nell’arco dell’intera esistenza dinamica degli ammassi stellari. Questo finché non si scoprì che essa era accresciuta dalla presenza dei buchi neri, molto comune in contesti stellari simili. Ulteriore motivo di passata indifferenza verso la 3BBF è rappresentato dalla convinzione che essa tenda ad avere come esito binarie “soft”, destinate cioè ad essere facilmente distrutte da successivi eventi perturbativi a causa della notevole distanza tracomponenti, contrariamente a quelle “hard”. Tuttavia, nonostante la scarsa longevità, le binarie soft si formerebbero così frequentemente che la probabilità che una piccola frazione di esse riesca a sopravvivere grazie ad un restringimento dell’orbita risulterebbe piuttosto elevata.

Ergo, ignorare il contributo della 3BBF nella realizzazione di modelli teorici sul ruolo dinamico della binarietà è sconsigliabile, benché obiettivamente vantaggioso in quanto limitante la complessità di calcolo e il dispendio computazionale. Infatti, le simulazioni a N-corpi richiedono algoritmi troppo elaborati per risolvere le interazioni a tre corpi in tempi accettabili e, viceversa, le tecniche Monte Carlo adottano semplificazioni spesso eccessive in vista di un’ottimizzazione della relativa performance. Un nuovo metodo di integrazione diretta sembra nondimeno in grado di superare tali difficoltà attraverso una rivisitazione del duplice lavoro di ricerca denominato AH76, il quale, basandosi su uno schema di campionamento Monte Carlo poco accurato, assumeva che la 3BBF avvenisse fra tre corpi inizialmente slegati (i.e., three unbound bodies, 3UB) di uguale massa e in modo non ricorrente. Mediante l’utilizzo dell’integratore TSUNAMI e del pacchetto Python CUSPBUILDING, il modello AH76 è stato quindi modificato correggendo le inconsistenze dell’inerente schema Monte Carlo e aumentando significativamente il numero di scattering 3UB per ottenere una più solida statistica. L’aggiunta delle espansioni post-newtoniane (i.e., metodi matematici per trovare delle soluzioni approssimate alle equazioni della relatività generale di Einstein) consente di includere nella trattazione della 3BBF pure i buchi neri e l’associata fenomenologia.
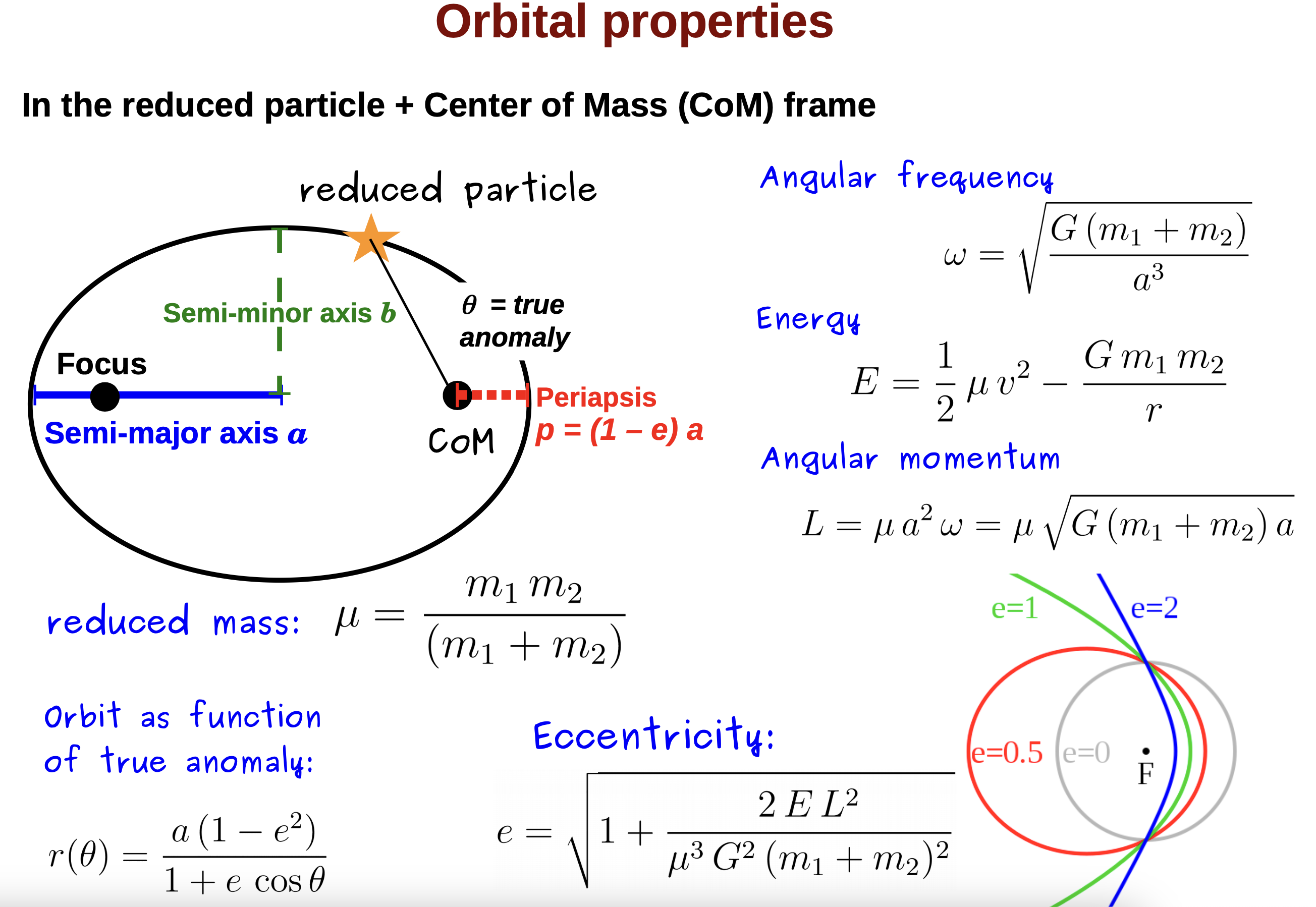
tipico codice simulativo a N-corpi: grazie alla riduzione al riferimento del centro
di massa (CoM), il sistema viene visto come un unico oggetto in dinamica
stellare. Crediti: Michela Mapelli.
Il primo evidente risultato dell’applicazione del così revisionato codice simulativo è che la 3BBF favorisce l’accoppiamento dei due corpi interagenti meno massivi nel caso delle binarie soft, e di quello più massivo con quello meno massivo nel caso delle binarie hard. Da notare, poi, che le prime, prodotte in percentuale molto più alta rispetto alle seconde, sono caratterizzate per lo più da orbite larghe ed eccentriche come quelle osservate dalla missione Gaia. Ciò conferma allora che, sebbene aventi un tempo di vita generalmente breve, alcune binarie soft comunque esistono: pertanto, ometterle dalla descrizione dello stato dinamico di un sistema stellare condurrebbe ad una visione parzialmente errata. Per converso, l’inserimento degli effetti post-newtoniani nella 3BBF stimola la generazione di binarie hard di buchi neri tramite l’emissione di onde gravitazionali che si verifica nel corso dell’interazione con il terzo corpo. Poiché questo canale di formazione acquista rilievo soltanto negli ammassi nucleari per via della loro notevole densità, si può tenere conto di questa declinazione della 3BBF in maniera selettiva. Qualora invece la 3BBF avvenga in ammassi globulari, con la sua tipica combinazione di due stelle di sequenza principale e un buco nero, si trova che le collisioni con altre stelle vicine non impattano fortemente sul processo purché esso abbia come frutto una binaria hard. Infine, si constata che il meccanismo della 3BBF promuove l’espulsione ad alta velocità del corpo catalizzatore, che può riuscire addirittura a scappare dall’ammasso ospite, divenendo perciò una stella fuggitiva (i.e., runaway star) all’interno dell’alone galattico. Ciò sembra valere specialmente per stelle catalizzatrici di sequenza principale, che lasciano di norma un neonato sistema binario hard composto o da una stella analoga e da un buco nero o da due buchi neri.
Riassumendo, questo studio dettagliato sulla 3BBF dimostra, in accordo con le premesse, l’importanza di non dare per scontato che fenomeni considerati meno probabili non incidano sulla determinazione dello stato fisico di un sistema stellare. Invero, a discapito dei vecchi pregiudizi scientifici, si conclude che una frazione di binarie soft non viene sciolta, essendo tuttora osservabile con i telescopi spaziali, che l’emergenza degli effetti post-newtoniani e delle collisioni dipende dalle proprietà ambientali, e che parte della popolazione di runaway stars nella Via Lattea risulta naturalmente spiegata. Eppure, questo non è altro che un mero punto di partenza: molto lavoro resta ancora da fare per esplorare tutte le sfaccettature del problema 3UB, che si configura come centrale per la comprensione della dinamica stellare. Si attendono dunque future e più sofisticate implementazioni di tale nuovo, promettente approccio simulativo per immergersi a fondo in questo affascinante settore fisico-matematico dell’odierna astrofisica teorica.
Fonte: arXiv.
Vuoi essere sempre aggiornato sul Cielo del Mese?
















