La Terra nel Sacco

Ah, quanto è difficile dare giudizi!

Come siamo soliti ricordare, quel che ci piace nei problemi e – soprattutto – nelle soluzioni, non è tanto l’esattezza del risultato, quanto il rassicurante rumor di meningi tutto teso all’assassinio d’un quesito e alla nascita d’una risposta. Se poi la risposta è giusta, tanto meglio: se non lo è, beh, quanto meno è importante che la ricerca sia stata gratificante per il ricercatore. La maggior parte delle scoperte si fanno fanno si sta cercando qualcosa d’altro.

Nell’ormai lontano Settembre, avevamo posto quattro quesiti relativi agli accadimenti che si possono osservare qualora si decida di cingere il nostro amato pianeta con coperte, sacchi, cinture e quant’altro. Le soluzioni sono arrivate copiose, anche se opportunamente variegate in merito ai quesiti stessi. Per non perdere troppo tempo in chiacchiere, ritorniamo alla prima delle quattro domande poste:

Primo e Secondo Quesito:

Chiedevamo di quanto sarebbe aumentato il volume del sacco che copre esattamente la Terra, qualora potessimo aggiungere un metro quadro a cotanta superficie. Detto in termini meno farraginosi, la domanda è semplicemente la seguente: “Di quanto aumenta V se A aumenta di 1 m2?“. La domanda successiva, del tutto conseguente, chiedeva “di quanto si sarebbe allora alzata la copertura dalla superficie della Terra“.

Sappiamo che:

e che:

da cui si ricava:

e anche:

Da qui si ottiene:

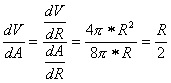
Che significa, all’incirca, 3,2 milioni di  metri cubi. Sembra un mucchio di spazio, ma se calcoliamo il raggio della corona sferica (per capire di quanto si alzerebbe il “sacco” dalla superficie terrestre), viene circa un nanometro. Una vera miseria.

Terzo Quesito:

Questo quesito è stato probabilmente confuso con un altro, essenzialmente più facile: non chiedevamo infatti di quanto si sarebbe alzata tutta la cintura dalla Terra, se avessimo allungato la cintura di 6 metri, ma bensì di quanto si sarebbe alzata in un solo punto, quello dove noi l’avremmo tirata verso l’alto. In altri termini, la cintura non doveva andare a posizionarsi come una specie di anello di Saturno tutta intorno (e sempre sollevata) dalla Terra; doveva invece restare sempre aderente al pianeta salvo nel punto in cui noi la sollevavamo verso l’alto e nelle vicinanze di quel punto. Se si fosse capito bene il problema, non ci sarebbe arrivata nessuna risposta del tipo “0.96 metri”, che è stata senz’altro la risposta più comune. Questo perchè basta immaginare “operativamente” come si potrebbe procedere all’esperimento vero e proprio. Avendo la Terra “ben cinturata”, potremmo tagliare la cintura in un punto qualsiasi, e lì operare la giunta di sei metri.
Mantenendo la cintura originale ancora aderente alla Terra, si può facilmente immaginare che la situazione sarebbe, in questo momento intermedio ancora precedente alla sollevazione, quella di una cintura ancora aderente con uno stretto cappio che sale ad una altezza di tre metri e poi ritorna in basso. A questo punto, infilando il dito nel cappio (alto già 3 metri, e quindi si capisce al volo che la risposta deve essere maggiore e non minore di 3 m) solleviamo la cintura in alto finchè questa non sarà bloccata dalla Terra
stessa, da qualche parte lontano oltre i due orizzonti. La risposta di questo problema è davvero sorprendente (e rendiamo merito a Piergiorgio Ferrante per averla mirabilmente sintetizzata), e si ottiene così:

Come inizia a dire lo stesso Piergiorgio:

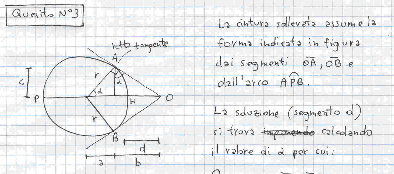
Dalla nostra figura si vede che abbiamo infilato il dito in S e, tirando, la cintura è diventata tangente in P e Q. Il raggio terrestre è r e l’altezza per cui abbiamo tirato su è h.

Quello che sappiamo é che r=6400 Km e che abbiamo aggiunto d=0,006 Km.
Lavorando in radianti,

e, considerando che per “tirare su” devo fare l’aggiunta, ho:

Inoltre,
e

da cui,

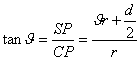
Il trucco per risolvere questa schifezza consiste nel ricordarsi della
Formula di Taylor:

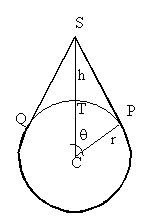
da cui

ossia,
radianti

ora, con lo stesso trucco per semplificarsi la vita, si ha:

…e, facendo i calcoli, h=401 metri circa. Da non crederci…

Quarto Quesito:

Andiamo un po’ di corsa,  ma davvero abbiamo poco spazio residuo, perdonateci:

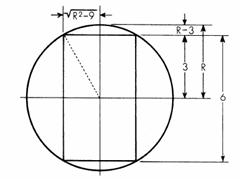
Dalla figura che segue, si vede che se R è il raggio del pianeta, le calotte sferiche e il cilindro restante devono avere le dimensioni indicate.

Per determinare il volume residuo, sottraiamo dal volume della sfera la somma del volume del cilindro e del doppio del volume della calotta sferica:

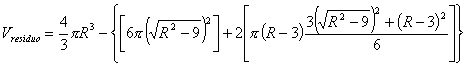
Svolgendo i calcoli, si vede che il risultato è
, ossia è
indipendente dal
raggio del buco o da quello della sfera!

Anche non ricordandosi le formule di cui sopra, “barando” leggermente è possibile risolvere il problema:

Il problema infatti non sarebbe posto se non avesse soluzione unica; se la soluzione è unica, il volume deve essere costante anche se il buco viene ad avere raggio zero; quindi il risultato deve essere pari al volume di una sfera di diametro 6, e quindi
.

Inutile chiedere quale sia la nostra soluzione preferita…

E non resta altro che salutarci, oramai…