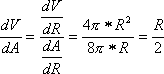La Terra nel Sacco

Quasi certamente ve ne stavate in spiaggia, a crogiolarvi come salamandre sotto il sole d’agosto. Quasi certamente la vostra attenzione era ben diretta verso pelli abbronzate o, al massimo, verso l’orizzonte lontano, a scrutare il lento variare delle nuvole. Eppure, nonostante la vostra colpevole indifferenza, nella splendida capitale della Repubblica Ceca, tra il 14 e il 25 agosto, i partecipanti al XXVI Congresso della IAU si sono ferocemente accapigliati nel tentativo di sciogliere il secolare dubbio sulla definizione di pianeta. Voi eravate forse al chiosco della spiaggia a sorbire un sorbetto, e loro concionavano sul raggio minimo ammissibile; voi vi riempivate i polmoni di iodio respirando l’aria salmastra e mostrando i pettorali, e loro si dannavano sul requisito della sfericità, o forse sulla necessità della complanarietà delle orbite.
Facile, adesso, dopo il sorbetto estivo, fingere di avere opinioni chiare e sicure su Plutone e gli altri transnettuniani; la verità è che non avete dedicato al fondamentale problema più attenzione di quanta ne riserviate di solito ad un sorbetto al limone.
Ed è facile dimostrarlo. Prendete il primo pianeta che vi capita sottomano, e vediamo quanto davvero lo conoscete. Per dirne una, vi ricordate di Vladimirov Javacheff Christo? È il tizio che da 30 anni continua imperterrito ad incartare qualsiasi cosa con fogli di vinile (monumenti, palazzi, gasometri, il Central Park addirittura) sostenendo che tali incartamenti siano Arte (siete pregati di notare la maiuscola). Bene, per mantenere sempre desta l’attenzione dei media, la tendenza del nostro artista sembra essere quella di cercare di incartare qualcosa di sempre più grande. Come credete che finirà? È evidente che, prima o poi, raggiungerà il limite, proponendo di incartare l’intero globo terrestre.
Supponiamo allora che questa grande opera d’arte incartatoria sia già terminata, e che la Terra sia stata perfettamente avvolta da una aderente pellicola di plastica. E supponiamo anche di aggiungere un metro quadro esatto a questa copertura, stando attenti a mantenerla perfettamente sferica; due domande, a questo punto, sorgono spontanee.
Considerando la Terra perfettamente sferica e con un raggio di 6400 km, che volume resta compreso tra la plastica e la Terra? Inoltre, appurato che (forse) per un po’ riusciremmo a respirare, vorremmo anche sapere se riusciremo ad alzarci in piedi, e quindi: quanto disterà la copertura di plastica dalla superficie della Terra?
Se incartare la Terra vi pare eccessivo, allora limitiamoci a cingerla con una elegante cintura lungo l’equatore (però questa non è Arte). Anche in questo caso, mossi a pietà da una troppo spietata aderenza, aggiungiamo 6 metri di cintura e, come ogni persona che finalmente non si sente stringere sulla pancia, infiliamo un dito sotto e tiriamo la cintura verso l’esterno.
Oddio, a dire il vero non sappiamo neppure se aggiungendo 6 miseri metri ad una cintura che di metri ne misura quaranta milioni, riusciremo mai a farci passare un dito… Ma insomma: supposto che il dito ci passi e che noi si riesca a sollevare la cintura, di quanto si alzerà la cintura dalla superficie della Terra?
È possibile che si rendano necessarie delle approssimazioni, per chiudere il calcolo, sapete? Già… un pianeta come la Terra sembra assolutamente ovvio e banale, eppure basta poco e torna ad essere misterioso. Eppure, se si affrontano i problemi con il giusto approccio, a volte si risolvono anche quelli che sembrano impossibili. Non ci credete? Considerate allora un altro pianeta (visto che quello che abbiamo è l’unico abitabile nei paraggi, e non vorremmo rovinarlo più dello stretto necessario) e scaviamoci un buco da parte a parte. Con un po’ di sorpresa, ci accorgiamo che questo buco, escludendo le calotte sferiche che abbiamo tolto da entrambe le parti per iniziare a scavare, ha una lunghezza di 6000 km esatti. Ecco, che ci crediate o meno, avete già tutti gli elementi necessari a stabilire quale sia il volume restante del pianeta.
Con il che fanno 4 domande che valgono un abbonamento semestrale a Coelum. Che state aspettando?