Dalle Stelle alle Stalle

Questa volta non possiamo proprio lamentarci. Per provarci, ci avete provato seriamente.
Come il nostro Direttore ha brutalmente e gordianamente riassunto, il problema si limita ad essere un quesito puramente geometrico: prendete un cerchio, fissate un punto qualunque della sua circonferenza, e da qui tracciate un opportuno arco tale da coprire un’area che divida il cerchio originario esattamente a metà.
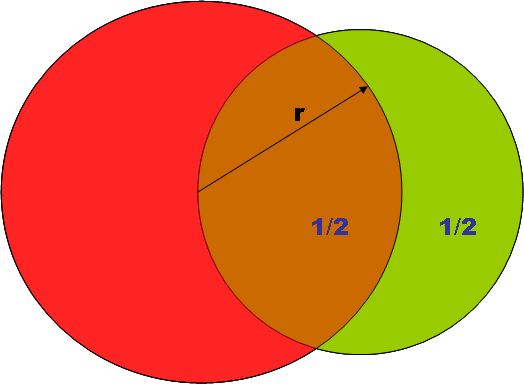
Insomma, dato il cerchio originario (verde) tracciarne un altro con centro sulla circonferenza del primo tale da dividere il cerchio verde in due sezioni equivalenti.
Così:

Il primo a provarci è stato Andrea Alessandrini, che però si è mostrato non solo veloce, ma anche astutamente pigro: anziché mandarci la soluzione, ci ha dato la URL dove trovarla:

http://spazioinwind.libero.it/alphard/AlessandriniA.jpg

Dania Nachira ha dato un contributo più esplicito (almeno nella forma di recapito):

Indichiamo con x la lunghezza della corda a cui è legato il mostro, supponendo che in questa lunghezza sia compresa anche la distanza tra il collo del mostro a cui è legata la corda e il suo muso.

A questo punto si impone che l’area divorata in un giorno sia uguale a p*r*r/2 (con r= raggio del disco solare e p= pi greco).
L’area divorata sarà uguale alla somma dell’area del settore circolare di raggio x (lunghezza della corda) e dei due segmenti circolari sottesi alla corde di lunghezza x (la somma di queste figure dà esattamente la parte mangiata del sole o meglio occultata dalla luna).

Risolvendo si ottiene la seguente equazione:

sen(p*r*r/2 + x*r sqrt(1- sqrt(2*r/x))- p/2*x*x) / sen(-x*x + r*r*2) = 2*r/x

dove, come precedentemente detto la risoluzione fornisce il valore di x=lunghezza della corda.

Dania ci dice di studiare medicina, e a noi piace molto l’idea di avere un futuro medico che si interessa sia di matematica che di astronomia. C’è davvero bisogno di scienza, in questo secolo.

Fabiano Limonio non è stato da meno: si è dato molto da fare, pur avendo a disposizione un tempo limitato per farlo:

Prendiamo una circonferenza di raggio r1 con centro M nell’origine degli assi. Prendiamo una seconda circonferenza di raggio r2, maggiore di r1, il cui centro, N, è all’intersezione della prima circonferenza con l’asse positivo x. Troviamo i due punti in cui si intersecano le due circonferenze, A e B. A questo punto abbiamo due settori circolari, uno delimitato dai punti MAB e l’altro NAB. I punti A e B formano un triangolo rettangolo con il centro delle circonferenze e la loro proiezione perpendicolare con l’asse x; si riesce a calcolare la loro area. Per calcolare l’area del settore circolare bisogna trovare l’angolo che dal centro delle circonferenze arriva ad A, o a B. Essendo in un triangolo rettangolo costante il rapporto tra un lato e il seno dell’angolo opposto, conoscendo noi esattamente le misure dei lati del triangolo rettangolo, riusciamo anche a trovarne gli angoli. Calcoliamo l’area del settore circolare del primo cerchio e gli togliamo i suoi triangoli rettangoli, facciamo lo stesso con il secondo cerchio e sommiamo i due risultati. Quest’ultimo dato deve valere metà dell’area del primo cerchio.
La formula che ne deriva è complicata e non so semplificarla, quindi per trovare il valore che deve avere la corda vado per tentativi (poco più del raggio del primo cerchio).

Va riconosciuto a Fabiano che la sua conclusione “poco più del raggio del primo cerchio” è qualitativamente corretta, anche se rimane non valorizzata. Il passo successivo, anche se è costato sudore, lo ha fatto infine una vecchia conoscenza:

Valerio Pecoraro (N.A. per gli amici del Forum Coelestis), come si dice nei film, colpisce ancora:

Questa volta siete stati davvero diabolici! Raramente ci si imbatte in problemi di così (apparente) semplice formulazione ma la cui soluzione si dimostra molto ardua e infarcita di ispidi calcoli. Il problema del pasto della mucca legata al bordo di un prato circolare è uno di questi. Ci ho perso due notti trovando alla fine null’altro che un’equazione trascendente, la cui soluzione è per definizione approssimata (sia pure con un margine piccolo a piacere). Forse esiste un altro metodo più elegante e più semplice. Anzi, sicuramente è così, dal momento che capita sovente di avventurarsi per il sentiero più arduo e tortuoso senza riuscire a vedere la via retta che si ha davanti agli occhi.
Dunque, Immaginiamo un prato circolare di raggio r sulla cui circonferenza è ancorata una corda di lunghezza R alla cui estremità è legata una mucca.
Quale dev’essere il rapporto T = R/r tale per cui la mucca riesca a brucare un’area del prato pari alla sua metà?
Facciamo intersecare due cerchi (il prato e l’area in cui può spostarsi la mucca legata), di raggio rispettivamente r ed R  e centri O₁ e O₂, nei punti P₁ e P₂. L’area della superficie S brucata deve essere pari a pr²/2 ed ha la forma di un ellissoide composto da due segmenti circolari S₁ e S₂ che hanno la base comune data dalla corda P₁P₂.
Indicando con 2a e 2b gli angoli al centro dei cerchi che sottendono rispettivamente S₁ ed S₂, l’area del segmento circolare S₁ sarà data dalla differenza tra l’area del settore circolare sotteso da 2a e l’area del triangolo P₁O₂P₂. Ovvero:
S₁ = (2a*R²/2) – (R²*sen2a/2) = R²/2 * (2a – sen2a)
Analogamente avremo:
S₂ = r²/2 * (2b – sen2b)
Pertanto l’area brucata S sarà:
S = S₁ + S₂ = R²/2 * (2a – sen2a) + r²/2 * (2b – sen2b) che deve essere uguale alla metà del prato, ovvero pr²/2.
Avremo dunque la condizione:
pr²/2 = R²/2 * (2a – sen2a) + r²/2 * (2b – sen2b)
Dividendo ambo i membri per r²/2 si ha:
p = R²/r² * (2a – sen2a) + (2b – sen2b)
Poiché abbiamo indicato il rapporto R/r con T, esplicando per T avremo infine:
T² = (p – 2b+ sen2b) / (2a – sen2a)
Ora, considerando il triangolo P₁O₁O₂, esso è isoscele con due lati uguali a r ed il terzo uguale a R. Se il suo angolo in O₂ è pari alla metà di 2a (ovvero a, esso sarà anche uguale all’angolo in P₁. Pertanto il suo angolo in O₁ (la metà di 2b, ovver b) sarà:
b = p – 2a.
Inoltre, tracciando l’altezza relativa a R dal suo vertice O₁, risulterà diviso in due triangoli rettangoli uguali nei quali il cateto minore (R/2) sarà uguale all’ipotenusa (r) per il coseno dell’anglo adiacente (a). Dunque avremo:
R/2 = r * cosa
da cui:
R/r = 2* cosa
ossia
T = 2* cosa
Sostituendo b e T nella equazione trovata per l’area S avremo:
4*cos²a = (p – 2(p – 2a) + sen2(p – 2a)) / (2*a – sen2a)
Semplificando si ha:
cos²a = (-p + 4a – sen4a) / (8*a – 4*sen2a)
Che è appunto un’equazione trascendente in funzione dell’angolo a.
Con successive iterazioni (moltissime, per la verità) si trova che il valore dell’angolo a che soddisfa questa uguaglianza oscilla intorno al valore medio:
a = 0,9528478647… espresso in radianti.
Il valore del rapporto T = R/r sarà:
R/r = 2*cos(0,9528478647) = 1,158728473…
Perché, dunque, la mucca bruchi un’area pari alla metà di un cerchio stando legata ad una corda ancorata sulla sua circonferenza, occorre che tale corda sia lunga circa 1,158728473 volte il raggio di tale circonferenza.