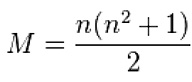Quadrati magici
La rubrica Moebius del numero di novembre parlava di quadrati magici. Per chi non ricordasse più di cosa si tratta, un quadrato magico è una sorta di matrice formata da n righe ed n colonne, le cui caselle sono riempite con tutti i numeri compresi tra 1 e n2, disposti in maniera tale che la somma dei numeri su ogni riga, su ogni colonna e su ciascuna delle diagonali produca sempre lo stesso numero.
Il “Lo Shu” di cui ho parlato nell’articolo è, di fatto, l’unico quadrato magico di lato 3.
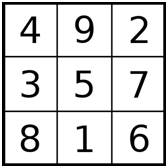Nel “Lo Shu”, la “costante di magia”, cioè il valore della somma ricorrente dei numeri delle righe, delle colonne e delle diagonali, vale 15, che corrisponde al numero di giorni in ciascuno dei 24 cicli dell’anno solare cinese. Come ricordavo nell’articolo di novembre, questo quadrato viene considerato un simbolo di armonia universale: i numeri presenti nelle sue caselle sono ritenuti dei portafortuna, soprattutto il 5 centrale.
Fateci caso: questo quadrato rimane magico anche se sottoposto a rotazione di 90°, a riflessione rispetto alla colonna centrale, o ad una sequenza di operazioni di questi due tipi.
In tutto possiamo generare 8 quadrati magici 3×3 apparentemente diversi: tuttavia, dal punto di vista dei matematici, le rotazioni e le riflessioni non variano nella sostanza la natura del quadrato magico, per cui si dice che esiste un unico quadrato magico di lato 3.
Non appena si considerano quadrati appena più grandi le cose cambiano. Per esempio, trascurando le rotazioni e le riflessioni, esistono ben 880 quadrati magici 4×4, e sono addirittura 275.305.224 le analoghe strutture con lato 5. E qui ci fermiamo, nel senso che non siamo in grado di quantificare i quadrati magici 6×6. E figuratevi quelli più grandi.
Il numero dei quadrati magici aumenta quindi rapidissimamente al crescere del lato. Una cosa è certa: dato un qualsiasi numero n maggiore di 2, è possibile costruire un quadrato magico nxn.
Un altro fatto è assodato: in un quadrato magico di lato n la “costante di magia” è calcolabile con la formula:
Particolarità nel quadrato di Dürer
Il celebre quadrato magico di lato 4 che compare nell’incisione “Melencolia I”, realizzata da Albrecht Dürer nel 1514, è testimonianza dell’interesse rinascimentale per questi bizzarri oggetti matematici.
Come accennavo nell’articolo, anche un matematico rigoroso come Luca Pacioli fu attratto dal fascino numerologico dei quadrati magici.
Nel trattato De viribus quantitatis scriveva infatti:
De li numeri in forma quadrata disposti secondo lastronomi figure deli pianeti cioe ch’per lato et diametri sempre fanno tanto, dove 3 a 9. si trovano quelli di ordine da 3 a 9
Il quadrato di Dürer gode di particolarissime proprietà matematiche. Per esempio, la costante di magia 34 può essere ottenuta non solo sommando i numeri sulle righe, sulle colonne e sulle diagonali, ma anche sommando i numeri dei quattro quadratini 2×2 che si possono ricavare all’interno del quadrato, e persino sommando i quattro numeri agli spigoli. Il quadrato, poi, è simmetrico, nel senso che la somma di un numero qualsiasi e del suo simmetrico rispetto al centro del quadrato dà sempre 17.
Come costruire quadrati magici piccoli e grandi
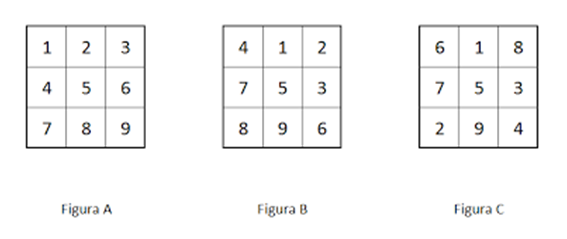
Volete imparare un piccolo “gioco di prestigio” da esibire orgogliosamente agli amici nelle serate piovose? Realizzate nove cartoncini quadrati, numerati con le cifre da 1 a 9. Disponeteli ora in ordine, come nella figura A. Ruotate ora i numeri esterni di una posizione, ottenendo la disposizione della figura B. Infine scambiate tra di loro i numeri posizionati sugli angoli del quadrato. Et voila, ecco il vostro quadrato magico 3×3: autentico, della pregiata famiglia Lo Shu!
Se però al fascino orientale dei quadrati 3×3 preferite il sapore rinascimentale di quelli 4×4, eccovi accontentati: preparate 16 quadrati con i numeri da 1 a 16, disponeteli in modo ordinato in uno schieramento 4×4 e poi invertite ciascuna delle due diagonali. Ecco servito il vostro quadrato magico di lato 4!
Lo so, l’appetito vien mangiando, e adesso vorreste che vi rivelassi il segreto per costruire con facilità quadrati magici di lato qualsiasi. Bè, non esageriamo: al crescere del lato le cose si fanno molto più difficili, e sono state ideate tecniche molto sofisticate per raggiungere questo obiettivo. Tra le metodologie più interessanti vi sono gli algoritmi genetici, che si ispirano ai meccanismi dell’evoluzione darwiniana per far “emergere” da uno spazio indistinto di possibili soluzioni quelle di qualità più alta (in bibliografia trovate una pagina che illustra questa tecnica per fare evolvere quadrati magici).
Il problema e la soluzione
Il problema di novembre consisteva nel trovare un oggetto di tipo 3×3 che è un parente dei quadrati magici, ma non è veramente magico: nelle sue 9 caselle devono trovare posto i numeri da 1 a 9, ma su ogni riga, su ogni colonna e su ogni diagonale, deve essere costante non la somma dei tre numeri (come nei veri quadrati magici), bensì la somma dei due numeri esterni meno quello centrale. Se volete, potremmo chiamare questo quadrato “sub-magico”.
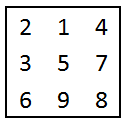Così come esiste un solo quadrato magico 3×3 (a meno di rotazioni e riflessioni), esiste un solo quadrato “sub-magico” 3×3 (vedi immagine qui a destra).
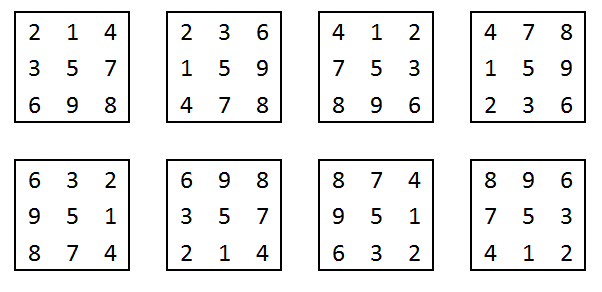
Anche in questo caso, si possono generare altri 7 quadrati sub-magici grazie alle rotazioni e alle riflessioni. Ecco tutte le soluzioni possibili:
L’unico lettore che ha inviato tutte e otto le soluzioni è stato Domenico Tumeo, al quale vanno le nostre più vive congratulazioni. Tuttavia il sig. Tumeo non è stato il più veloce a inviare la sua e-mail, e per aggiudicarsi l’abbonamento bastava anche un solo quadrato sub-magico. Il primo ad arrivare in redazione è stato quello di Giorgia Hofer, che però aveva già vinto l’abbonamento con l’enigma di ottobre. Il vincitore di novembre è risultato quindi SERGIO SCALENGHE (che ha anche inviato, seppure in ritardo, una soluzione dell’enigma del mese di ottobre).
Hanno inviato soluzioni corrette anche i lettori Marco Carnevale, Andrea Chiaramonte, Michele d’Errico e Fabio Nevola.
Complimenti a tutti questi… magici lettori!
Letture consigliate
- Martin Gardner, Enigmi e giochi matematici, Milano, Rizzoli, 2001.
- Dal blog Popinga di Marco Fulvio Barozzi: Quadrati magici e pensiero occulto
- Dal blog thesciencebookstore.com: Magical magic square of some advanced age
